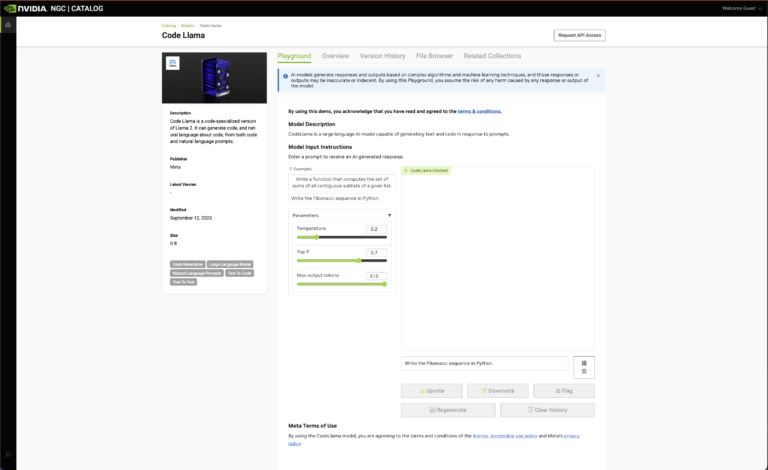
Big O notation with examples
Response from ChatGPT
Here are some more examples for each algorithm:
O(1) – Constant Time
- Accessing a specific element in an array by index.
- Performing basic arithmetic operations (e.g. addition, subtraction, multiplication, division) on two numbers.
- Retrieving the size of a container (e.g. an array, list, or dictionary) in Python using the
len()function.
O(log n) – Logarithmic Time
- Binary search on a sorted array of elements.
- Finding an item in a balanced binary search tree.
- Computing the value of x to the power of n using exponentiation by squaring.
O(n) – Linear Time
- Finding the maximum or minimum element in an unsorted array.
- Counting the number of occurrences of a specific element in an array.
- Copying the elements of one array to another.
O(n log n) – Linearithmic Time
- Sorting an array using merge sort or quicksort.
- Heapifying an array.
- Computing the convex hull of a set of points in two-dimensional space using the Graham scan algorithm.
O(n^2) – Quadratic Time
- Selection sort.
- Bubble sort.
- Insertion sort.
- Computing the dot product of two vectors.
- Checking if a given string is a palindrome using brute force.
O(2^n) – Exponential Time
- Generating all subsets of a set.
- Solving the traveling salesman problem using brute force.
- Computing the Fibonacci sequence using recursive function calls.
It’s worth noting that in practice, the actual running time of an algorithm can depend on various factors such as the input size, the specific implementation, and the hardware it’s running on. The big O notation provides a useful approximation of how the running time of an algorithm scales with input size, but it doesn’t provide a complete picture of the algorithm’s performance.
References:
- Big O notation: https://en.wikipedia.org/wiki/Big_O_notation
- Sorting algorithms: https://en.wikipedia.org/wiki/Sorting_algorithm
- Convex hull algorithms: https://en.wikipedia.org/wiki/Convex_hull_algorithms
- Traveling salesman problem: https://en.wikipedia.org/wiki/Travelling_salesman_problem
- Fibonacci sequence: https://en.wikipedia.org/wiki/Fibonacci_number